Newton's Law of Universal Gravitation
Isaac Newton compared the acceleration of the moon to the acceleration of objects on earth. Believing that gravitational forces were responsible for each, Newton was able to draw an important conclusion about the dependence of gravity upon distance. This comparison led him to conclude that the force of gravitational attraction between the Earth and other objects is inversely proportional to the distance separating the earth's center from the object's center. But distance is not the only variable affecting the magnitude of a gravitational force. Consider Newton's famous equation
Fnet = m • a
Newton knew that the force that caused the apple's acceleration (gravity) must be dependent upon the mass of the apple. And since the force acting to cause the apple's downward acceleration also causes the earth's upward acceleration (Newton's third law), that force must also depend upon the mass of the earth. So for Newton, the force of gravity acting between the earth and any other object is directly proportional to the mass of the earth, directly proportional to the mass of the object, and inversely proportional to the square of the distance that separates the centers of the earth and the object.
But Newton's law of universal gravitation extends gravity beyond earth. Newton's law of universal gravitation is about the universality of gravity. Newton's place in the Gravity Hall of Fame is not due to his discovery of gravity, but rather due to his discovery that gravitation is universal. ALL objects attract each other with a force of gravitational attraction. Gravity is universal. This force of gravitational attraction is directly dependent upon the masses of both objects and inversely proportional to the square of the distance that separates their centers. Newton's conclusion about the magnitude of gravitational forces is summarized symbolically as
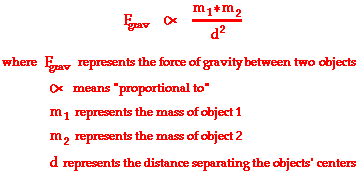
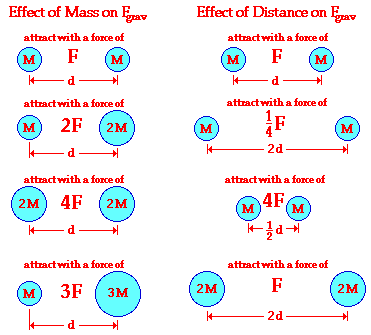
Since the gravitational force is directly proportional to the mass of both interacting objects, more massive objects will attract each other with a greater gravitational force. So as the mass of either object increases, the force of gravitational attraction between them also increases. If the mass of one of the objects is doubled, then the force of gravity between them is doubled. If the mass of one of the objects is tripled, then the force of gravity between them is tripled. If the mass of both of the objects is doubled, then the force of gravity between them is quadrupled; and so on.
Since gravitational force is inversely proportional to the separation distance between the two interacting objects, more separation distance will result in weaker gravitational forces. So as two objects are separated from each other, the force of gravitational attraction between them also decreases. If the separation distance between two objects is doubled (increased by a factor of 2), then the force of gravitational attraction is decreased by a factor of 4 (2 raised to the second power). If the separation distance between any two objects is tripled (increased by a factor of 3), then the force of gravitational attraction is decreased by a factor of 9 (3 raised to the second power).
The proportionalities expressed by Newton's universal law of gravitation are represented graphically by the following illustration. Observe how the force of gravity is directly proportional to the product of the two masses and inversely proportional to the square of the distance of separation.
Another means of representing the proportionalities is to express the relationships in the form of an equation using a constant of proportionality. This equation is shown below.
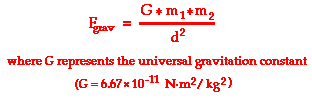
The constant of proportionality (G) in the above equation is known as the universal gravitation constant. The precise value of G was determined experimentally by Henry Cavendish in the century after Newton's death. (This experiment will be discussed later in Lesson 3.) The value of G is found to be
G = 6.673 x 10-11 N m2/kg2
The units on G may seem rather odd; nonetheless they are sensible. When the units on G are substituted into the equation above and multiplied by m1• m2 units and divided by d2 units, the result will be Newtons - the unit of force.
Knowing the value of G allows us to calculate the force of gravitational attraction between any two objects of known mass and known separation distance. As a first example, consider the following problem.
Determine the force of gravitational attraction between the earth (m = 5.98 x 1024 kg) and a 70-kg physics student if the student is standing at sea level, a distance of 6.38 x 106 m from earth's center. |
The solution of the problem involves substituting known values of G (6.673 x 10-11 N m2/kg2), m1 (5.98 x 1024 kg), m2 (70 kg) and d (6.38 x 106 m) into the universal gravitation equation and solving for Fgrav. The solution is as follows:
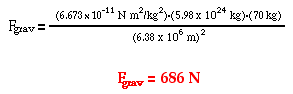
Determine the force of gravitational attraction between the earth (m = 5.98 x 1024 kg) and a 70-kg physics student if the student is in an airplane at 40000 feet above earth's surface. This would place the student a distance of 6.39 x 106 m from earth's center. |
The solution of the problem involves substituting known values of G (6.673 x 10-11 N m2/kg2), m1 (5.98 x 1024 kg), m2 (70 kg) and d (6.39 x 106 m) into the universal gravitation equation and solving for Fgrav. The solution is as follows:
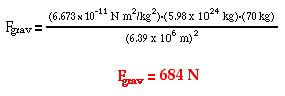
Two general conceptual comments can be made about the results of the two sample calculations above. First, observe that the force of gravity acting upon the student (a.k.a. the student's weight) is less on an airplane at 40 000 feet than at sea level. This illustrates the inverse relationship between separation distance and the force of gravity (or in this case, the weight of the student). The student weighs less at the higher altitude. However, a mere change of 40 000 feet further from the center of the Earth is virtually negligible. This altitude change altered the student's weight changed by 2 N that is much less than 1% of the original weight. A distance of 40 000 feet (from the earth's surface to a high altitude airplane) is not very far when compared to a distance of 6.38 x 106 m (equivalent to nearly 20 000 000 feet from the center of the earth to the surface of the earth). This alteration of distance is like a drop in a bucket when compared to the large radius of the Earth. As shown in the diagram below, distance of separation becomes much more influential when a significant variation is made.

The second conceptual comment to be made about the above sample calculations is that the use of Newton's universal gravitation equation to calculate the force of gravity (or weight) yields the same result as when calculating it using the equation presented in Unit 2:
Both equations accomplish the same result because (as we will study later in Lesson 3) the value of g is equivalent to the ratio of (G•Mearth)/(Rearth)2.

Sir: What causes gravity?
ReplyDelete@megumi: What causes Gravity?
ReplyDeleteOne of Einstein's old tutors, a man by the name of Minkowski showed that the special theory of relativity could be expressed in an interesting way.
The world we live in consists of four dimensions, the three space dimensions and one that is not exactly time but is related to time (it is in fact time multiplied by the square root of -1). This is not at all easy to understand but it means that space-time as we call it has some rather weird properties. In particular, when you move through one of the space dimensions you also travel, unwittingly, through time. You do not notice this, indeed as far as you are concerned nothing happens to you at all, but someone observing you would say that you have travelled through time. Of course, we are always travelling through time, but when you travel through space you travel through time by less that you expect. The most famous example of this effect is the "Twins Paradox".
All the effects of special relativity, such as the slowing down of clocks and the shrinking of rods follow from the above. In fact, it is often better to think of some things, such as electromagnetic fields as being four-dimensional objects. However, the important thing to remember for the moment, is: when you move through space you are compelled to move through time but, when you move through time (which of course you are always doing) you do not have to move through space.
So, what does this have to do with gravity? It is quite simple! When a mass is present in the above space-time it distorts it so that whilst it remains true that travelling through space causes you to travel through time, travelling through time now causes you to move (accelerate) through space. In other words just by existing, you are compelled to move through space - this is gravity.
The particular advantage of this theory of gravity (General Relativity) is that it explains, at a stroke, all the observed properties of gravity. For example the fact that it acts equally on all objects and substances becomes obvious when you thing of gravity as a distortion of space-time rather than a force.
Imagine that you are in free space, away from any planets or stars, when suddenly a planet is created quite close to you. You would not be aware that anything is happening to you, you would feel no force, but you would find that you started to accelerate towards the planet. This is just like the case where you travel through space, you are not aware that you have also travelled through time but people observing you are.
Can you feel gravity?
You can argue that we do not. What happens is that, as you pass through time, the distortion of space-time caused by the presence of the earth accelerates your body towards the centre of the earth. However, when your feet are touching the ground, the ground exerts a force on your feet in an upwards direction which pushes you in the opposite direction. In other words you are being accelerated upwards with respect to space-time by the force of the ground acting on your feet. It is exactly the same as the force which seems to push you back in your car seat when you accelerate, what is really happening is that the seat is pushing you forwards.
HOW IMPORTANT GRAVITY IS?
ReplyDelete